Binary Heap (이진 힙)

힙은 아래 성질을 만족하는 Alomost complete binary tree이다.

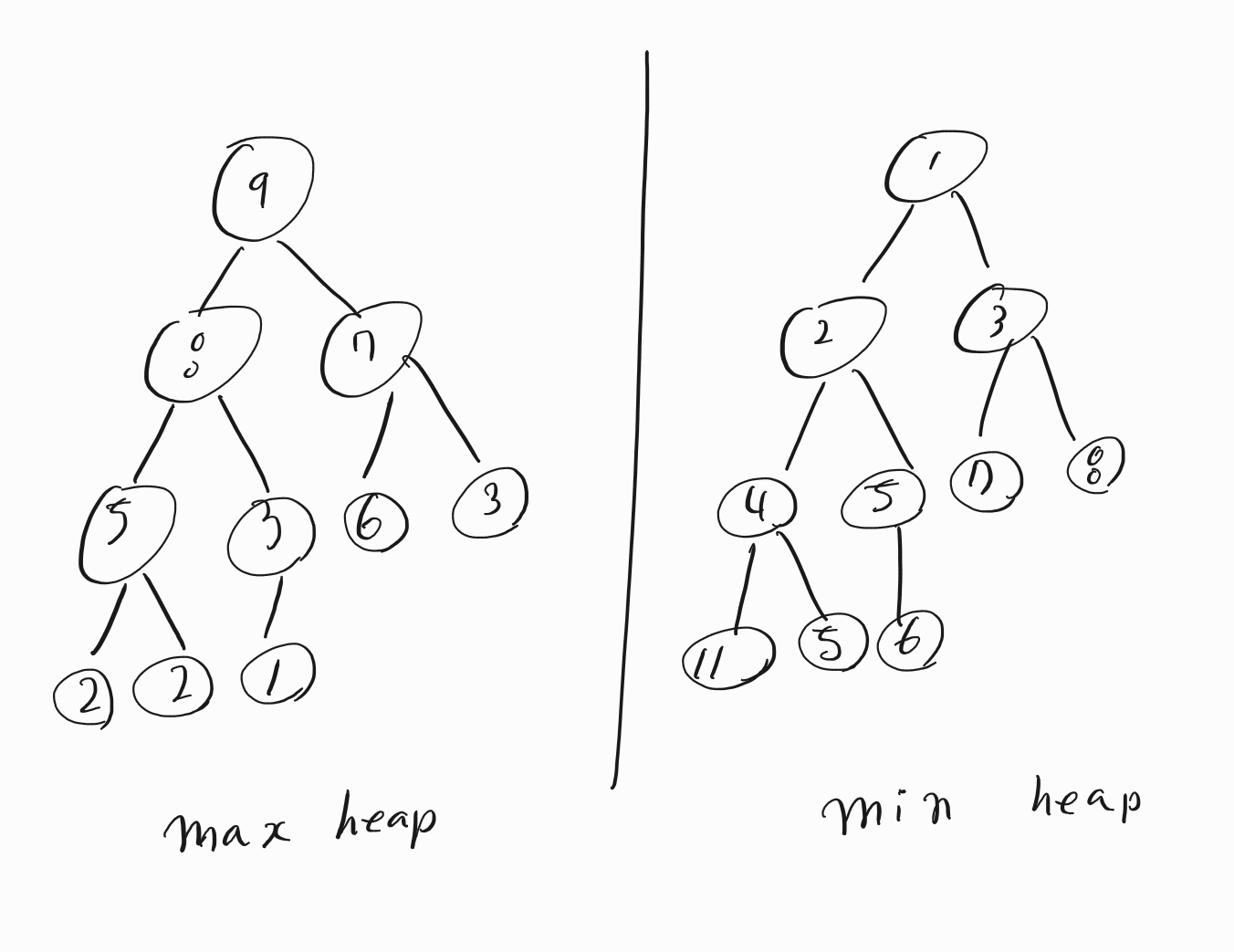
Max heap의 경우 parent node의 값은 child node의 값보다 크거나 같다.
Min heap의 경우 parent node의 값은 child node의 값보다 작거나 같다.

아래의 모든 설명은 Max heap을 기준으로 한다.

Max heap의 경우 tree 내의 모든 노드에 대해 parent node의 값은 child node의 값보다 작지 않다. 그래서 Max heap에선 root node의 값이 가장 크다. 값을 삽입하고 뺄 때도 이 성질을 유지하면 root에서는 항상 tree 내의 가장 큰 값이 존재하게 된다. Cpp의 priority queue를 사용해 본 적이 있는가? 어떤 값을 priority queue에 넣고, pop()으로 빼더라도 priority queue의 top()은 항상 그때그때 내부에서 가장 큰 값을 반환한다. 이 priority queue는 heap으로 구현되었다.

구현

Heap은 Almost complete binary tree이다. 아까 heap의 그림을 보면 tree가 depth가 낮은 node 들부터, 왼쪽부터 오른쪽 순서대로 차 있는 것을 볼 수 있다. 덕분에 배열을 사용한 tree 구현으로 특정 index의 node를 쉽게 접근할 수 있게 된다. 또, 배열 내에서 1번부터 heap 내부 값의 개수만큼 값들이 빈 곳 없이 연속적으로 존재하게 된다.

구현의 편의상 배열의 0번째 index가 아닌 1번째 index를 tree의 root으로 삼도록 하겠다. i번째 index에서 왼쪽 자식의 index는 2*i이고 오른쪽 자식의 index는 2*i+1이 된다.

값의 삽입 (push)

heap에 어떤 값을 넣어보자. 우리는 지금 Max heap을 구현하고 있고, parent node는 항상 child node보다 작으면 안 된다는 점을 기억하자. 아래의 과정에 의해 삽입이 이루어진다.

tree의 맨 마지막에 넣고자 하는 값 x를 삽입한다.
방금 삽입한 node에서 parent를 확인하고, parent의 값이 x보다 작으면 두 노드의 위치를 교환한다.
2번 과정을 parent node의 값이 x보다 작지 않거나 현재 노드가 root 노드가 될 때까지 반복한다.

위 과정을 짧게 말하면 삽입하고자 하는 값을 tree의 가장 마지막에 넣고, heap의 성질을 만족할 때까지 위로 올려주는 것이다.

아래 예시를 보자. heap에 9를 삽입하는 과정이다.

그림의 1번에선 tree의 맨 마지막에 값을 삽입한다.
그림의 2, 3번은 parent node와 확인 후 parent 노드가 자신보다 작았기 때문에 위치를 바꿔주는 과정이다.
그림의 4번에서는 parent node의 값이 자신보다 크기 때문에 두 노드의 위치를 바꿔주지 않아도 된다.

위 과정을 코드로 쓰면 아래와 같다.

void push(int x) {
    data[++size] = x;
    int tmp;

    for (int i = size, parent = size >> 1; parent != 0 && data[parent] < data[i]; 
        i >>= 1, parent >>= 1){
        swap(data[parent], data[i]);
    }
}

이 과정의 시간복잡도는 O(logn)이다. 트리의 높이에 비례하여 적절한 노드의 위치를 탐색하기 때문이다.

최댓값 조회 (top)

Max heap에서 최댓값을 조회하기 위해서는 root node의 값을 보기만 하면 된다.

int top() const { return data[1]; }

시간복잡도는 O(1)이다.

최대값 제거 (pop)

Max heap에서 root node의 값을 제거하고, 다시 heap의 성질을 만족하기 위해 tree를 조작해 주는 과정이다.

root node의 위치에 tree의 마지막 값을 넣어주고, 기존에 있던 마지막 값은 제거한다.
현재 node를 root로 설정한다.
현재 node가 left, right 두 child의 값보다 크다면 둘 중 값이 큰 node와 위치를 변경한다. 만약 right 노드가 존재하지 않는다면 left 하고만 비교하여 수행한다.
3번 과정을 child의 값 중 큰 값이 현재 노드보다 작거나 left, right 두 child 모두 존재하지 않을 때까지 반복한다.

위 과정을 짧게 말하면 가장 마지막 값을 root에 넣고, 그 값을 heap의 성질을 만족할 때까지 아래로 내려주는 것이다.

그림의 1번은 tree의 마지막 값을 root에 넣고, 마지막 node를 제거하는 모습이다.
그림의 2,3,4는 child와 비교하여 두 child 중 큰 값이 현재 노드보다 크다면 위치를 바꿔주는 모습이다.
그림의 4번에서 위치를 변경하고 난 후 더 이상 child 현재 노드에 child 가 존재하지 않기 때문에 과정을 종료한다.

void pop() {
    data[1] = data[size--];

    for (size_t i = 1, left = i << 1, right = left | 1; // left = i*2, right = i*2+1
         left <= size;
         left = i << 1, right = left | 1) {

        // left child is bigger than right child or right child does not exist
        if (left == size || data[left] > data[right]) { 
            if (data[i] < data[left]) { // left child is bigger than current node
                swap(data[i], data[left]);
                i = left;
            } else { 
                break;
            }
        } else { // right child is bigger than left child
            if (data[i] < data[right]) { // right child is bigger than current node
                swap(data[i], data[right]);
                i = right;
            } else {
                break;
            }
        }
    }
}

시간복잡도는 push때와 같은 이유로 O(logn)이다.

heapify

어떤 노드 x가 있고, x의 left, right child를 각각 root로하는 subtree가 heap의 성질을 만족할 때, x를 root로 하는 tree도 heap이 되도록 하는 연산을 heapify라고 한다.

사실 이는 우리가 pop을 수행하였던 과정에 포함되어 있다. pop을 수행할 때 우리는 root에 tree의 가장 마지막 값을 넣고, 마지막 값을 지웠다. 그전에 root의 left, right child를 root로 하는 subtree는 힙의 성질을 이미 만족하고 있었다. root에 다른 값을 넣음으로 트리 전체에 대해서는 힙의 성질을 만족하지 않게 되지만, root의 left, right subtree는 여전히 heap의 성질을 만족하는 것이다. 이후 수행된 작업은 root node에 대해서 heapify를 수행한 것이다. 만약 임의의 node에 대해 heapify를 수행하고자 한다면 아래처럼 코드를 짤 수 있다.

void heapify(int idx) {
    for (size_t i = idx, left = i << 1, right = left | 1;  // left = i*2, right=i*2+1
         left <= size;
         left = i << 1, right = left | 1) {
        // left child is bigger than right child or right child does not exist
        if (left == size || data[left] > data[right]) {
            if (data[i] < data[left]) {  // left child is bigger than current node
                swap(data[i], data[left]);
                i = left;
            } else {
                break;
            }
        } else { // right child is bigger than left child
            if (data[i] < data[right]) {  // right child is bigger than currentnode
                swap(data[i], data[right]);
                i = right;
            } else {
                break;
            }
        }
    }
}

heapify를 사용해서 pop을 다시 작성해 보자.

void pop() {
    data[1] = data[size--];
    heapify(1);
}

임의의 complete binary tree를 heap으로 변경하기

heap을 만족하지 않는 complete binary tree를 heap으로 변경해 보자. heapify를 사용하면 간단하게 구현할 수 있는데, 코드는 아래와 같다.

void tree2heap(){
    for(int i=size/2; i>0;--i){
        heapify(i);
    }
}

size/2 번 노드부터 1번 root 노드까지 heapify를 반복하면 된다. size/2 + 1 번 이후로는 child node가 존재하지 않기 때문에 수행하지 않아도 된다. index가 낮아질수록 depth 값이 작은 곳에 노드가 있고, index 값이 큰 수부터 진행하기 때문에 i번째 node에 대해 heapify를 수행할 때는 이미 그들의 child를 root로 하는 subtree들이 heap의 성질을 만족하고 있다.

시간복잡도는 어떨까? O(logn) 연산을 n/2번 반복하였으므로 O(nlogn) 이다. 그런데, 조금 더 타이트하게 생각해 보면 위 방법으로 O(n)에 해결할 수 있다는 결론이 나온다.

깊이가 1인 node의 수는 n/2^h개이다.
깊이가 2인 node의 수는 n/2^(h-1)이다.
...
깊이가 h인 node 수는 n/2^(0) = n/2 개이다.

깊이가 d인 노트들은 높이가 h-d인 tree에 대해서 heapify 연산을 수행하게 될 것이다. 어떤 깊이 노드 수와 그 깊이에서 heapify 연산을 수행하는 tree 깊이를 곱하고, 깊이별로 이를 구하고 합해서 정리하면 아래와 같다.

코드

아래는 위 코드들을 단순히 합쳐놓은 코드이다.

#define MAX_N 100000

inline void swap(int &a, int &b) {
    int tmp = b;
    b = a;
    a = tmp;
}

class MaxHeap {
    int data[MAX_N + 1];
    size_t size;

   public:
    MaxHeap() {
        size = 0;
    }

    void clear() { size = 0; }

    bool empty() { return size == 0; }

    void push(int x) {
        data[++size] = x;
        int tmp;

        for (int i = size, parent = size >> 1; parent != 0 && data[parent] < data[i]; i >>= 1, parent >>= 1) {
            swap(data[parent], data[i]);
        }
    }

    int top() const { return data[1]; }

    void pop() {
        data[1] = data[size--];
        heapify(1);
    }

    void heapify(int idx) {
        for (size_t i = idx, left = i << 1, right = left | 1;  // left = i*2, right = i*2+1
             left <= size;
             left = i << 1, right = left | 1) {
            // left child is bigger than right child or right child does not exist
            if (left == size || data[left] > data[right]) {
                if (data[i] < data[left]) {  // left child is bigger than current node
                    swap(data[i], data[left]);
                    i = left;
                } else {
                    break;
                }
            } else {                          // right child is bigger than left child
                if (data[i] < data[right]) {  // right child is bigger than current node
                    swap(data[i], data[right]);
                    i = right;
                } else {
                    break;
                }
            }
        }
    }

    void tree2heap(){
        for(int i=size/2; i>0;--i){
            heapify(i);
        }
    }
};

'Study > Algorithm & Ds' 카테고리의 다른 글

Disjoint Set (Union find) (0)	2023.05.01
Binary Search, 이진탐색 (0)	2023.01.06
Next permutation, 다음 순열 구하기 (0)	2022.04.04
Merge Sort (합병 정렬) (0)	2021.09.17
Fenwick Tree (펜윅 트리, Binary Indexed Tree = BIT) (0)	2021.05.13

Temp

Binary Heap (이진 힙)

구현

값의 삽입 (push)

최댓값 조회 (top)

최대값 제거 (pop)

heapify

임의의 complete binary tree를 heap으로 변경하기

코드

'Study > Algorithm & Ds' 카테고리의 다른 글

댓글

티스토리툴바

Binary Heap (이진 힙)

구현

값의 삽입 (push)

최댓값 조회 (top)

최대값 제거 (pop)

heapify

임의의 complete binary tree를 heap으로 변경하기

코드

'Study > Algorithm & Ds' 카테고리의 다른 글

관련글

댓글

티스토리툴바